ギフチョウ出現グラフについて
　越冬したギフチョウ蛹がいつ羽化するか、当然気温が関係する。ただし、ある気温になったら羽化するといものではないだろう。例えば、ずっと5℃が続き、ある日20℃になったからといって羽化するわけではないからである。「ある温度」を越え、それからの気温の積み重ねに関係するのだろう。

　蛹のいる場所の気温は、その近辺にある気象庁のアメダスデータを代用するしかない。ただしアメダス装置の設置場所は風通しがよく、日差しをさえぎるものがない場所で、気温は地上高1.5mで測定される。一方、蛹のいる場所（ほとんど地面）の気温はアメダスデータより最高気温は低く、最低気温は高いと聞く。

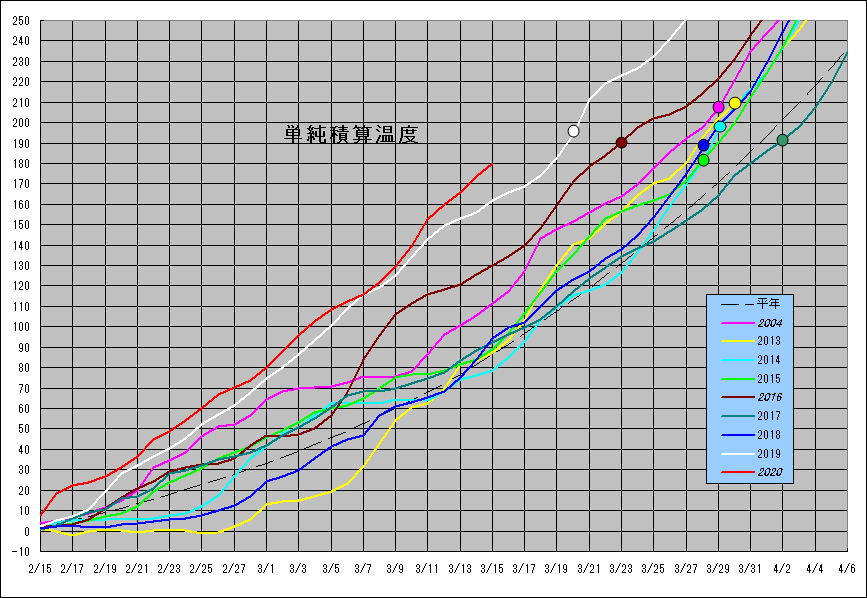
　今年も、例年のごとく上記「ある温度」になる日を2月1日として、日平均気温を使用して2020年の気温データ加えてみた。気温の積み重ねは単純に日平均気温を積算する方法である。昨年はこの方法で2月1日からの積算温度グラフに過去の出現記録日を各年ごとにプロットしたグラフを作成し、予想してきたが、ここにきて出現温度のバラツキが気になりだした。もちろん過去の出現日が初見日とは限らない。ネット情報の最も早い日にすぎないし、天候（日差し）の影響をうけてしまう。さらに、この方法であると、蛹のいる場所ではそうでもないであろう突出値（春一番などによる1〜2日程度の高温）の影響がそのまま積算値に影響し、出現日温度がかなりばらついてしまうし、予想を2、3日早めてしまう。前述の蛹のいる場所の気温とアメダスデータの違いにもよると考えるが、実際に合わそうと、今回、突出値を抑える積算方法として当該日と前後1日のMEDIAN値を当該日の気温として、その積算値によってグラフを作成してみたが、バラツキはかえって大きくなってしまった。理由は？である。

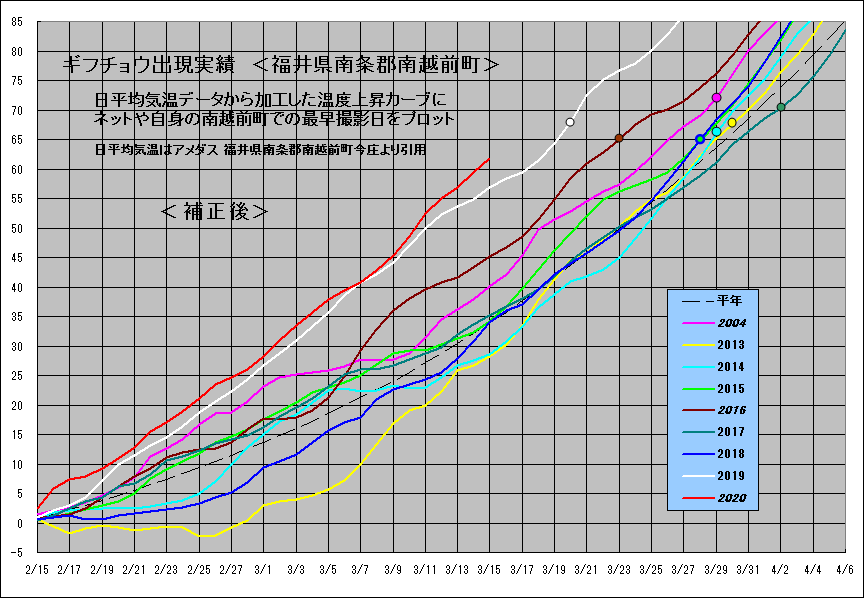
　そこで、日平均気温の1未満のべき乗をとることとし、カットアンドトライにて0.62乗値が一番バラツキを抑え、いい感じのグラフとなることがわかった。ただし、マイナス値の1未満のべき乗値は虚数となってしまうので、期間中の最低マイナス気温値をあらかじめすべてのデータに加算してから0.62乗値を求め、加算による影響を取りのぞくため、0度が0度となるように固定値を差し引いた。

　　　　変換気温＝(当該日の日平均気温＋期間中のマイナス気温最低値)＾0.62−1.49

上記変換気温値の積算値をグラフ化した。